Spring 2020 Semester-COVID-19 Project at Home
Spring 2020 semester was challenging at an unprecedented time due to COVID-19. The students' creativity to apply the knowledge that they have learned in face-to-face and online classes in the absence of laboratory equipment were unique and impressive in a lot of different ways.
FLUID MECHANICS CREATE-A-LAB-UW-PLATTEVILLE-SPRING 2020
Turbine Generated Power-Spring 2020
The objective of this project is to determine whether a turbine will create more power from water flowing through the turbine or water falling on the turbine. A closed system, for example a tube with water flowing through it connected to a turbine, will create more power when compared to an open system, for example water cascading off a cliff to a turbine at the bottom. To test which turbine had more power in the lab our team assembled a container to act like a dam. On side had a gutter with no slope, which gave results due to pressure head, and one with a 70-degree slope which gave represented the water falling off a cliff. Both were tested with the same turbine assembly so that the results would not be skewed. The revolutions of the turbine and the flow of water were used to determine which turbine positioning was more effective. The results proved our hypothesis wrong. After four trial runs for a 0º slope and a 70º slope, the 70º slope resulted in an average of 64.25 revolutions, while the 0º slope resulted in an average of 58.75. This concludes to the open channel providing more energy.
Force of Waterjet from a Garden Hose-Spring 2020
The force that a water jet produces is critical in the design of many apparatuses in everyday life
such as firefighting hoses, irrigation systems, mining operations, water jet cutting machines, and garden
hoses. The objective of this experiment was to determine the force that a typical garden hose water jet
can produce by using the linear momentum equation. This was achieved by measuring the time it takes
to fill a 5 gallon bucket, measuring the inside diameter of the hose, and taking the temperature of the
water. This data was used to calculate the force of the water jet from the garden hose. The results of the
lab indicate that the garden hose tested produced a force of 0.083 lbf.
Spring 2020
Viscosity Based on Different Temperatures-Spring 2020
Viscosity Based on Different Temperatures-Spring 2020
Viscosity Based on Different Temperatures-Spring 2020

Viscosity is due to an internal force that is affected by the state of being thick, sticky and semifluid in its consistency. The objective of this lab was to determine the effect of temperature on the viscosity of a fluid. The hypothesis was that all fluids will experience a lower viscosity when the temperature is higher than room temperature compared to when their temperatures are at room temperature or below room temperature. An equation for viscosity was not readily available, therefore velocity was calculated to determine relative viscosity trends. This was based on the assumption that viscosity and velocity are inversely related. To perform this experiment, first angle a cooking pan at 45-degrees, with a piece of paper taped to the back and covered smooth in saran wrap. Perform the tests by recording the time the fluid takes to travel from one end of the 8”x11.5” paper to the other end. The results confirmed and validated the hypothesis. A fluid, such as honey, was recorded traveling the length of the paper on average at 116.07 seconds while colder than room temperature. Then, while at a warmer temperature than room temperature, the honey had an average time of 0.48 seconds. Therefore, as the temperature becomes higher for the fluid, the velocity increases which correlates to a lower viscosity, and vice versa.
Force of Waterjet from a Garden Hose-Spring 2020
Viscosity Based on Different Temperatures-Spring 2020
Viscosity Based on Different Temperatures-Spring 2020

The force that a water jet produces is critical in the design of many apparatuses in everyday life
such as firefighting hoses, irrigation systems, mining operations, water jet cutting machines, and garden
hoses. The objective of this experiment was to determine the force that a typical garden hose water jet
can produce by using the linear momentum equation. This was achieved by measuring the time it takes
to fill a 5 gallon bucket, measuring the inside diameter of the hose, and taking the temperature of the
water. This data was used to calculate the force of the water jet from the garden hose. The results of the
lab indicate that the garden hose tested produced a force of 0.083 lbf.
Siphon Experiment at home-Spring 2020
Viscosity Based on Different Temperatures-Spring 2020
Pressure Differences, Flow Classification, and Head Loss in a Garden Hose- Spring 2020

Siphons have been used since very early times as a practical and inexpensive way to move water from place to place. Gravitational forces and pressure variations are the factors that allow the siphon to be successful. The objective of this lab experiment was to examine how different liquids, gas and water, flow through the siphon. This lab experiment was performed by using two measuring glasses, a 0.5-centimeter diameter clear tube, and a pipette. Once a measuring glass was placed at a higher elevation than the other and filled with the desired liquid, one end of the tube was placed into the elevated glass, while the other end of the tube was placed in the lower glass. Then, suction was applied to the exposed end of the tube until a steady flow of liquid was achieved. A stopwatch was used to determine the flow rate. The results of this lab indicated that gasoline was able to achieve a higher flow rate and velocity than water. The average velocity of gasoline at the exit of the siphon was 0.359 m/s, while the average velocity of water was 0.314 m/s. This can be expected because gasoline is less dense than water. Reynolds number for gasoline was determined to be 4642 and waters Reynolds number was 3884. Therefore, both liquids were in turbulent flow.
Pressure Differences, Flow Classification, and Head Loss in a Garden Hose- Spring 2020
Pressure Differences, Flow Classification, and Head Loss in a Garden Hose- Spring 2020

The objectives of the lab were to determine velocity, flow rate, major and minor losses of two water flows out of a garden hose and prove that fluids with a higher velocity have lower internal pressure compared to those with a lesser velocity. Required materials included a garden hose, thermometer, PVC pipe, food coloring, tape measure, and stopwatch. Lengths and diameters of the garden hose and PVC pipe needed to be collected. The procedure of the experiment involved adding food coloring to water running through the PVC pipe and timing how long it took the water to reach the end of the pipe. The process was completed 6 times for two different flows. With a known length of PVC pipe and average time for each flow, average velocity and flow rates were calculated (flow 1: 2.88 ft/s, 0.0245 ft3/s and flow 2: 3.40 ft/s, 0.0272 ft3/s). Using Bernoulli’s equation and the average velocities, the pressure difference between the two flows was calculated to be 1.84 psf. Therefore, the theory that pressure is inversely related velocity was proven. The higher the velocity is for a flow of water, the lower the internal pressure is, which explains why faster moving flows of water stream farther and straighter than slower flows. Furthermore, the hose diameter and velocities were used to calculate Reynold’s Number and classify each flow. Each flow was classified as turbulent as the Reynold’s Numbers for flows 1 and 2 were 9,760 and 10,819, respectively. Lastly, the length and diameter of the garden hose were used with the flow velocities to calculate major and minor head loss within the hose for each flow of water (flow 1: 0.826 ft, 0.141 ft and flow 2: 0.916 ft, 0.174 ft). The values were added together to calculate total head loss for flow 1 (0.968 ft) and flow 2 (1.090 ft).
Fluid Properties of Household Liquids-Spring 2020

There are a seemingly infinite amount of liquids in the world. Many of them one can find in their home. Our team set out to find the fluid properties of some common household liquids. Properties measured include viscosity, specific gravity, and surface tension. To accomplish this task, a home experiment was conducted. A large clear water bottle would be filled with a given fluid. A bead with measured density was dropped into the liquid and timed to see how long it would take for the bead to fall from one mark to the next. From there, the velocity of the bead can be calculated. The fluid density would also be calculated by knowing the volume and weight of the liquid. From knowing the bead density, liquid density, and bead velocity, the dynamic viscosity of the liquid can be calculated. Also, from knowing the liquid’s density, the specific gravity of the fluid can be calculated. Surface tension can be calculated by putting a straw into a liquid and seeing how high the capillary rise is. Surface tension is calculated using the capillary rise, density, and radius of the straw. These properties were then tabulated and compared.
Hydropower Dam Energy Production-Spring 2020

The purpose of this experiment was to determine the feasibility of converting the Indian Ford River Dam into a hydroelectric power supply using a turbine. The experiment was conducted by using Bernoulli's equation to determine the head loss due to the turbine and the power was calculated using the turbine power equation. Some design assumptions needed to be made due to our inability to physically take measurements of the dam. Power was calculated using both high and low flows of the river to show a range of power production. The power calculated in megawatts was then converted to equivalence in number of people the hydropower dam would service with electricity. It was concluded that the use of a turbine to harness hydroelectric power would be a feasible and recommended action.
Spring 2020
Pressure Added per Pump-Spring 2020
Pressure Added per Pump-Spring 2020
Pressure Added per Pump-Spring 2020

The objective of this lab was to determine the pressure added per pump of a water gun by
using Bernoulli’s equation and kinematics. To determine the pressure added per pump, a water gun
was placed on an elevated surface at a certain height, pumped a certain number of times, shot, and
then the max distance of the water traveled was recorded. The experiment consisted of two rounds.
The only difference between them was the water guns elevation. Then the first kinematic equation
was used to calculate time of travel. The second kinematic equation calculated the max velocity of the
water. Lastly, Bernoulli’s equation was used to determine the pressure inside the water gun.
At-Home Hydraulic Lift -Spring 2020
Pressure Added per Pump-Spring 2020
Pressure Added per Pump-Spring 2020

The purpose of this lab experiment was to create a model hydraulic lift to demonstrate the applications of pressure in the real world. This was completed by using different sized syringes to see how heavier objects can be lifted from the difference in pressure within syringes. The use of Pascal’s Principle shows the force it takes to lift a certain amount of weight for each different sized syringe.
Pressure Measurement-Spring 2020
Pressure Added per Pump-Spring 2020
Testing Viscosities of Multiple Materials-Spring 2020

Bernoulli’s Equation is a simple but powerful tool that can be used to find pressure, velocity, and elevation. The objective of this experiment was to determine the pressure at the end of the hose. This was achieved by filling a 55-gallon drum with the hose set at 45 psi. The head loss and velocities were calculated after the experiment. The results found by this experiment revealed that the pressure at the end of the hose was 43.4 psi. The pressure was lower than the initial pressure of 45 psi due to major and minor head losses that occurred through the hose.
Testing Viscosities of Multiple Materials-Spring 2020
Determining Viscosity of Water, Oil and Syrup-Spring 2020
Testing Viscosities of Multiple Materials-Spring 2020

The purpose of this experiment is to further understand viscosity of various liquid (i.e. water, oil, etc.) by developing an experimental procedure that uses Stokes’ Law. Viscosity is defined as the internal resistance of a fluid to motion and is expressed as the ratio of shear stress to the rate of deformation. The goal of this experiment was to obtain viscosities of household liquids using Stokes law. Through ten trials of dropping a bead in a tube of water, oil, and soda water and measuring the time it takes to drop a known distance. An average mass and radius for the ten beads is found, with each bead being used being one of the ten trials. By measuring volume and mass of each liquid, a density of the liquids can be calculated. This same process can be repeated for the beads to find their density as well. Once all these values are obtained, Stokes law is utilized to find the dynamic viscosity of each liquid. The results of this experiment yielded that the dynamic viscosity of water at 20° C is 0.040575 kg/m*s, for oil at 21° C is 0.108484 kg/m*s, and for soda at 10.5° C is 0.051442 kg/m*s.
Determining Viscosity of Water, Oil and Syrup-Spring 2020
Determining Viscosity of Water, Oil and Syrup-Spring 2020
Determining Viscosity of Water, Oil and Syrup-Spring 2020

The objective of this experiment was to determine the viscosity of water, oil and syrup by analyzing data and utilizing stokes’ law. This was accomplished by dropping identical metal BB’s into various jars that contained different liquids and each of which had different viscosities. The jars would be full of a liquid and each jar would have an area marked off in which the lab group would record the time it took for a BB to fall through it. The area that was marked off varied depending on what liquid was in the jar. When the BB’s traveled through the 10w-30 motor oil, the time it took for a BB to fall 5 inches was recorded. When the BB’s traveled through the syrup, the time it took the BB’s to descend through 4 inches was also recorded. The time it took for the BB to travel through 6 inches of water was also documented. This test would be repeated 10 times per jar for all 3 jars in order to obtain good data. When the lab was done and all of the calculations were completed, some groups found that the percent error is high. The reason for this is due to the many complications that this lab involves. Some factors for error could be that the metal BB’s do not fall straight down. This extra motion could increase the BB’s traveling time. Human error could be to blame as well when it comes to timing the BB’s descent through the marked off zone. Due to the factors of error, some variation in the experimental data should be expected.
Flow Rate of Different Styles of Inlet Castings-Spring 2020
Determining Viscosity of Water, Oil and Syrup-Spring 2020
Determining Viscosity of Water, Oil and Syrup-Spring 2020

The objective of this experiment was to find the best inlet casting design that allowed the fastest flow rate while not letting an excessive amount of debris through. In order to determine which inlet casting was the best, velocity of flow would have to be determined. Velocity plays a vital role in the experiment because if the inlet has a slow flow velocity, then water could pool up and cause flooding which could lead to different infrastructure problems. Another aspect that affects the flow rate is debris in an inlet. The purpose of the casting design is to allow water to flow in while keeping debris out. Procedure of this experiment was as follows: Cut out an inlet design in four different 5 gallon buckets, one design being five 8” long by 1” wide rectangular slits, another design having nineteen equally spaced 1” diameter circles, the next design being five equally spaced 3” diameter circles, and the last being nineteen 1” squares equally spaced throughout the bottom of the bucket. After the designs were cut out, three trials were conducted on each bucket for each test conducted. The first test was simply pouring 3 gallons of water into each bucket and timing how many seconds it took to completely empty. The second test was adding in ¾” gravel into each bucket and pouring in 3 gallons and again timing how long it took for the water to filter through. Along with timing how long the water took to filter through, amount of debris that stayed in the bottom of the bucket was counted. The buckets were also tested with sticks and leaves following the same steps and data collection. After all data was collected and analyzed, flow rate was found by taking 3 gallons, converting the gallons to cubic feet, then dividing by the time it took to filter through the bucket (in seconds). Velocity of the flow was then determined by taking the flow rate and dividing it by the total area of all openings in the casting.
Welcome
University of Wisconsin-Platteville emphasizes undergraduate education that provides technical excellence with a significant emphasis on real-world applications. The Fluid Mechanics project aim is to involve students in a strong hands-on curriculum to integrate the concepts students have learned in the class with the real application design. This project is an excellent opportunity to develop a junior-level design. All engineering projects required teamwork and collaboration. Fluid Mechanics project might be a good practice.
Photo Gallery-Fluid Mechanics Final Project
SELECTED FLUID MECHANICS Final PROJECTS
Innovative Blue Power with Mini Water Turbine
Application of Losses in Designing a Water Slide-F2018
Application of Losses in Designing a Water Slide-F2018

With knowledge of Climate Change it is of utmost importance to innovate alternative power sources to produce electricity. The project's purpose was to create a solution to aid society's need for electricity and determine if the system will generate enough power to charge a cell phone. The group used an orifice apparatus to simulate a household object such as a bucket. The turbine was then connected to the end of the orifice apparatus and water was sent through the turbine. The team applied Bernoulli's Equation to determine the power generated in the turbine, along with a voltage meter to confirm the efficiency of the device. The height of the water was set, and flowrate was determined to find the power the turbine could generate. The results showed that although the turbine generated power, the turbine was not efficient in converting the potential power to actual power generated. This discrepancy can be attributed to a multitude of reasons such as friction losses, turbine efficiency, and/or measuring methods. Although the data from the project was not as expected, it shows that apparatuses such as the one created below, in the design, are possible to construct and therefore the idea is an innovative advancement in alternative power.
Application of Losses in Designing a Water Slide-F2018
Application of Losses in Designing a Water Slide-F2018
Application of Losses in Designing a Water Slide-F2018

For the final project Sliders chose to make a mini model for a water slide. The objective of this lab was to determine how slide shape and head loss affected the discharge velocity at the bottom of the slide while having a balanced flow (steady-state). The original hypothesis for this experiment was that the depth of the pool would change a minuscule amount in order for the system to run at a steady-state and as the flow rate increased, the velocity would also increase at the discharge point. The different slide types (described below) would create different major and minor losses which were calculated. The equipment necessary for this experiment included plastic tubing to create a “mini” water slide, a place for water to pool (the hydraulic bench), a pump to create flow, pipe fittings, a stopwatch to measure the rate at which the water was flowing, and a yardstick to measure depth of the pool and the height of the slides.
Comprehensive Fluid Mechanics Lab Device-F2018
Application of Losses in Designing a Water Slide-F2018
Comprehensive Fluid Mechanics Lab Device-F2018

Learning Strategies LLC created and tested a lab experiment that tested several aspects of Fluid Mechanics. The purpose of this project was to create a lab for collegiate students that more directly applies to the concepts of a Fluid Mechanics class than what is currently in use. The topics covered by the lab consisted of the resultant force, Bernoulli’s equation and jet trajectory. The lab includes a device that models a dam gate as analyzed in the class’s homework and lecture. It also contains a jet created by a nozzle and the set up allows Bernoulli's equation to be used to analyze a standard hydraulic bench pump.
Site Content
Ram-Pump Efficiency and Head-S2019

The Purpose of this laboratory experiment was to test the ram pump for its efficiencies rates compared to the ratio of output to input heads. This was accomplished by running the ram pump using different heights for the output head (Garden Hose), while keeping the input head constant, except for the largest output head trial where the input head needed to be increased. Efficiency was determined by capturing the water that was successfully sent through the pump and the water that was wasted.
Relationship Between Pipe Roughness, Flow Velocity, and Head Loss-S2019

Darcy’s Equation states that the total head loss of a fluid travelling through a piping system is directly proportional to the velocity of a fluid and a unique “friction factor” that is directly proportional to the absolute roughness coefficient of the material of the pipe in which a fluid travels through. The purpose of this project was to investigate and verify if a direct relationship existed between the roughness of a pipe material and a fluid’s total head loss and between fluid velocity and a fluid’s total head loss. To achieve this, two separate experiments were conducted in which a fluid’s total head loss was determined as it traveled between two points in a ductile iron, a copper, and/or a PVC pipe of equal length and diameter in a head loss apparatus. The secondary objective of this project was to calculate the average experimental roughness coefficient of ductile iron, copper, and PVC pipes and to compare these values with theoretical values.
Experimental results revealed that fluid travelling through the ductile iron pipe was consistently subjected to the highest head loss of the three materials tested, while fluid travelling through the copper pipe was consistently subjected to the lowest head loss of the three materials tested. Average experimental absolute roughness coefficient values obtained for ductile iron, copper, and PVC pipes differed from theoretical values by approximately 21%, 22%, and 182%, respectively. Experimental results also revealed that the total head loss of a fluid travelling through a PVC pipe increased at a near steady rate as fluid velocity increased through four trials but surprisingly decreased as fluid velocity increased in two further trials. Despite the presence of some erroneous values in experimental data, results generally proved the concept that the roughness of a pipe material and the velocity of a fluid are directly proportional to the head loss a fluid is subjected to in a piping system.
Major and Minor Head Loss in a Piping System-S2019
Compare Head Loss Across Pipes Made of Different Materials-S2019

The purpose of this experiment was to calculate the major and minor losses in a piping system along with comparing the theoretical minor loss coefficient versus the experimental minor loss coefficient. This was done by first designing a piping system with five 90° smooth bend flanged elbows and two flanged branch flow tee joints, as seen in Figure 1. Along with the piping system a hydraulic bench and a bench top orifice apparatus was used. With this lab and knowledge from lecture regarding head loss, Reynold’s number, and Bernoulli’s Equation, the understanding of how to calculate and to determine how major and minor losses act on a system should be more clear. When comparing the theoretical and experimental minor loss coefficients of the apparatus and piping system the data provided results for the minor loss coefficients within a 30.1% error. In order to obtain more accurate results, it was determined that a longer piping system could be used since the short system that was used might not obtain a large head loss to begin with.
Compare Head Loss Across Pipes Made of Different Materials-S2019
Compare Head Loss Across Pipes Made of Different Materials-S2019
Compare Head Loss Across Pipes Made of Different Materials-S2019

The objective of this project was to calculate and compare head loss across pipes made of different materials and with different diameters. In this project the pipes used were as follows: one half-inch PVC, one half-inch iron, one five-eighths-inch iron, and one half-inch copper. For this, the change in pressure and flow rate were measured, and calculations were made to determine the theoretical and experimental head losses. Overall, the experiment was successful in determining and comparing the head losses in the PVC, one half inch iron, and copper pipes; however, the experiment was not successful in determining the head loss in the 5/8” iron pipe, having an approximate error of one hundred percent.
Pelton Wheel Turbine-S2019
Compare Head Loss Across Pipes Made of Different Materials-S2019
Head Loss of the Pump in the Fluid Mechanics Laboratory-S2019

The purpose of this report is to relay results from a student designed lab. The lab was designed to record the necessary data that would help to calculate the Output Shaft Power and Maximum Power Output of a Pelton Turbine. This was done by connecting the Pelton Turbine to a hydraulic bench in the fluids lab in order to record revolutions per second and flow rate. Another objective of the lab was to compare the Output Shaft Power and the Maximum Power Output. The results showed that the Output Shaft Power is 0.242 Watts while the Maximum Power Output for this particular Pelton Turbine is 91.8 Watts. What this means will be discussed in the analysis portion of this report.
Head Loss of the Pump in the Fluid Mechanics Laboratory-S2019
Compare Head Loss Across Pipes Made of Different Materials-S2019
Head Loss of the Pump in the Fluid Mechanics Laboratory-S2019

The objectives of the lab were to determine head loss of a pump by using Bernoulli’s equation, and to find the horsepower of the pump during the experiment. The procedure included the use of the pump in the open channel system, measuring the lengths of the piping, and counting the number of elbows and valves for total head loss calculations. The head loss of the pump was then calculated using Bernoulli’s Equation, and the horsepower was calculated after that. Schematics for the specific pump used in the experiment were researched online and then compared with the experimental data. When comparing the manufacturer data with the data found during the lab, a relatively large percent error was observed. However, the pump was not run at its ideal efficiency, so some variation in data was expected.
Site Content
Dam on Lake Mirflores-S2019
Head loss of Differing Filter Media-F2018
Head loss of Differing Filter Media-F2018

A dam is a barrier that stops or restricts the flow of water or underground streams. Reservoirs created by dams not only suppress floods but also provide water for activities such as irrigation, human consumption, industrial use, aquaculture, and navigability. Hydropower is often used in conjunction with dams to generate electricity. A dam is real world application of fluid mechanics. Determining the hydrostatic force and pressure to hold back water are major calculations conducted, as well as determining the dimensions for the damn, determining the flow rate going through the turbines, and determining the velocity going through the turbine.
Head loss of Differing Filter Media-F2018
Head loss of Differing Filter Media-F2018
Head loss of Differing Filter Media-F2018

The design consisted of several pieces of PVC pipe measured and connected to each other, while filter media was placed in between the pieces. Construction took place in the Engineering Hall shop utilizing multiple machines to cut and drill the piping. Pipes were then sanded and filed to achieve snug fits into holes and were then epoxied together. The purpose the apparatus was to find the minor losses created by the filter in the system. Multiple types of media were used inside of the filter which showed changed in pressure head for both upstream and downstream. Pitot tubes were used to find pressure heads before and after the filter. The polyester media was found to have a higher impact on head loss compared to the scouring media. Hydraulic conductivity values for the polyester and scouring media were 0.9704 and 1.204 in/s
D Pump Storage Hydropower System-F2018
Head loss of Differing Filter Media-F2018
Building a Dam for the Cedar River-F2018

A pumped storage hydropower system is a source of renewable energy that uses an elevation difference in water to produce electricity. The Bernoulli's equation was the key to determine the correct variables needed to design this system. A prototype was built and tested to ensure the correct equations were in use to design a full-scale system to produce enough power for a single-family house.
Building a Dam for the Cedar River-F2018
Building a Dam for the Cedar River-F2018

The purpose of this design project is to introduce the idea of building a dam for the Cedar River. The design of this new dam will help prevent flooding problems in nearby cities from heavy rain fall. The purpose of the concrete dam is to hold back water to a certain point. Once the water approaches the top of the dam, a pipe near the top will carry the water to the other side of the dam. This will cause the water to flow more slowly to the other side. Complete construction and no leaks in the system is necessary. Disregarding this may lead to erosion problems around the flow way or flooding in the nearby cities.
Hydroelectric Power-F2018

A client representing a city is in pursuit of a renewable energy source. Looking to utilize the nearby water source, a river, the client contracted with the Dam Engineers to design and present the plausibility of installing a hydroelectric dam to produce clean, renewable energy for the client’s city.
The purpose of the project is to consider the constraints and power requirements of the city and design a hydroelectric dam that will produce the proper output. The city has a unique restriction on the area of the output of water. Due to this constraint, the variable left to be determined will be the amount of head to maintain behind the dam to create the proper flow into the turbines.
To test the plausibility of a hydroelectric dam, Dam Engineers created a scaled model of the dam and turbine combination. A holding tank with an orifice was used to represent the dam itself, PVC pipe connections was used to represent the piping system, and a small turbine was used to extract energy from the water and convert it to electricity. Some key data collected during the design process include the turbine head (ht) value of the turbine, the efficiency needed to produce enough power .
Fighting the Fire-F2018

Through a series of 5 trials, flow of the water was found as well as the pump power to determine if this model would be dependable and work in the field. To replicate a real-life model that firefighters use to fight fires with and how a firefighting operation could determine how long their water reserves will last.
Site Content
Varying Friction Factors-S2019
Application of Force from a Jet Nozzle-F2018
Head Loss within Cast Iron Piping-S2019

In the modern world, varying pipes are used for many different purposes. Different materials have different properties that allow them to be used in a broad range of applications. Walking into the utility room in a first-world house, it is apparent how many different kinds of pipes are used right above/below everyone’s feet. The objective of this lab is to determine the most efficient materials. Copper, CPVC, and clear vinyl tubing were the three pipe materials tested. This was double the velocity calculated for copper. The group used a garden hose connected to a control valve to
Page 3 of 9
control the flow into each pipe tested. Each pipe tested was taped down onto a level surface to ensure accurate results an eliminate error. A constant flow rate was used for all tests, the water was sent through each pipe and into a graduated cylinder. The team applied Colebrook’s equation and Reynolds number to determine the most efficient material. The average velocity calculated for CPVC and clear vinyl tubing ranged from 8 to 9 m/s. The results showed that the calculated average friction factor for the copper, CPVC, and clear vinyl pipes were 0.0238, 0.0227, and 0.0218 respectively.
Head Loss within Cast Iron Piping-S2019
Application of Force from a Jet Nozzle-F2018
Head Loss within Cast Iron Piping-S2019

The purpose of this lab was to determine the head loss in the piping system that discharges into
the open flow channel device in the fluid mechanics laboratory. Piping systems are implemented
across a wide array of industries, including but not limited to wastewater treatment, farm field
irrigation, manufacturing, and residential housing. Head loss is a key consideration when
designing a piping system because it is a significant contributor to the efficiency of the system.
Flow rate and output frequency were measured and recorded. From here the continuity equation,
energy equation, and Reynolds number were used to find the pressure at the pump and head loss
at the discharge point. The head loss at a pump output of 29 Hz was found to be 2.11 ft.
Overall, the experiment showed that the piping system for the open channel flow device is
subject to a minimal amount of head loss and the pressure experienced within the system is
nearly negligible.
Application of Force from a Jet Nozzle-F2018
Application of Force from a Jet Nozzle-F2018
Application of Force from a Jet Nozzle-F2018

To begin, the group used the fluid calculation of the water force exerted on an object to find how much lift a Hydraulic Jet would have at different flows and nozzle sizes. By designing a Hydraulic Jet with interchangeable nozzles, the group was able to conduct a trial of different experiments to see if the group was able to match the applications of water jetpacks. The group started with a low flow and used all four nozzle sizes. The group found that at the lowest flow, none of the nozzles caused moving of the jet. As the group increased the flow, the group discovered that the jet would move the most at low flow speeds and low nozzle head. However, the smaller nozzle sizes caused more shaking than the larger ones that had a smooth, straight lift. Once the group tested four different flows, the group found the max flow rate that each nozzle could handle and the height it would reach.
Open Channel Flow – Reynold's Number-S2019
Application of Bernoulli’s Principle in Designing a Ram Pump-F2
Application of Force from a Jet Nozzle-F2018

This report focused on the type of flow (laminar, transitional, or turbulent) produced by different shaped outflow plates. The structures used were circular, 90° wedge, and square in shape. During this lab, we used the hydraulic bench, outlet plates, a piezometer, a meter stick, and a stopwatch to gather the information required to find the resulting Reynold’s number for each outflow through the three different shaped plates. The reason the group chose to perform this lab was because it was understood that it would help give clarity to why engineers use each type of outflow structure shape in certain situations. For example, it is apparent that engineers tend to favor rectangular outflow shapes when a higher volume of water needs to be transported. In addition, it is common for engineers to use circular outflow structures when directing storm water in urban areas. Given these two analyzations, it raises the question: does a required flow type determine the shape of the outfalls?
Through the analysis of the results, it becomes clear that the most effective outflow structure shape, by resulting in the least turbulent flow, is square. This is followed by the 90° wedge. Lastly, the least effective in limiting turbulence of the outflow is a circular shaped outflow structure. The resulting Reynold’s numbers are as follows: 9943, 10642, and 12851. These numbers were then compared to the open channel flow turbidity thresholds and concluded upon.
Hydraulic Press-F2018
Application of Bernoulli’s Principle in Designing a Ram Pump-F2
Application of Bernoulli’s Principle in Designing a Ram Pump-F2

A hydraulic press is a simple yet interesting machine that involves a fundamental concept of fluid mechanics. The objective of this project is to design and operate a hydraulic press that would not only challenge our strengths but also enhance our understanding of Pascal’s Law. The original objective was to be able to crush a soda can through a series of syringes and tubing. Due to unsatisfactory materials, the focus shifted to determining why the tubing could not handle the amount of pressure put upon it. The hydraulic press was built by using a series of syringes and tubes that would be given a known force on the top syringe. Using Pascal’s Law, the pressure was easily calculated and results can be viewed under the discussion heading. In conclusion, although we encountered adversity with our project we overcame it with credible results that further improved our understanding of the fluid mechanics concepts.
Application of Bernoulli’s Principle in Designing a Ram Pump-F2
Application of Bernoulli’s Principle in Designing a Ram Pump-F2
Application of Bernoulli’s Principle in Designing a Ram Pump-F2

Ram pumps are very environmentally friendly by using entirely renewable sources of energy. The purpose of the project was to design an economical ram pump in which could fill a storage tank from a river source without the use of electricity. While testing the ram pump, different designs were attempted until the pump was finally glued together with the best available design, mainly made of PVC pipe. The pump was then tested in the field using various hoses and a large water container as the reservoir. During testing, the team determined the pump had to be manually primed at the start in order to begin building pressure. The discharge hose was then taken up a ladder to simulate the elevation change from a river to a storage tank. Flow rate was then able to be recorded for the water coming out of the discharge hose varying from an average of 0.0002244 to 0.0003995 cubic feet per second. A trend that was seen was the efficiency of the pump continually decreased as the elevation difference of the pump and storage tank increased. Efficiency was then calculated with the highest being approximately 4%. This efficiency could be improved easily by using better materials on the pump and having a more consistent flow of water into the pump.
Selected Fluid Mechanics Projects
Application of Pascal’s Law in Designing Hydraulic Car Lift-F2018
Application of Bernoulli’s Principle: Water Shooter Design-Fall208
Application of Pascal’s Law in Designing Hydraulic Car Lift-F2018

In this project, the relationship of Pascal's law was used to create a car lift. This was done by creating a smaller scale, simplified version of a car lift. The lift is then tested using weights to measure the change in force. This is compared to theoretical values and error is calculated from experimentation. It was found that a greater area difference would be needed to achieve the results desired.
Nine Layer Density Tower Test and Orifice Shape Testing-F2018
Application of Bernoulli’s Principle: Water Shooter Design-Fall208
Application of Pascal’s Law in Designing Hydraulic Car Lift-F2018

The idea of the two tests were centered on the buoyancy lab and the orifice lab that were completed in Fluids CEE 3300. The first test was a 9-Layer Density Tower that tested the densities of 7 objects that were dropped within a density tower. Another objective of this test was to make a hypothesis about the density of the item before it was submerged in the liquid and test to see where it fell within the tower. The second test was testing to see if the change of shape of the orifice would affect the flowrate and if the change in diameter size and shape would make the discharge coefficient vary.
Application of Bernoulli’s Principle: Water Shooter Design-Fall208
Application of Bernoulli’s Principle: Water Shooter Design-Fall208
Application of Bernoulli’s Principle: Water Shooter Design-Fall208

The project addressed the issue of developing a simple, practical water shooter. The design of the shooter was based on the use of Bernoulli’s equation. Additional constant acceleration equations were utilized in the calculations. Theoretical data for the prototype was compared to experimental data and percent errors were derived. This design highlighted fundamental principles in fluid dynamics and displayed a thorough understanding of Bernoulli’s equation, as it relates to water jet trajectory.
Pumping Water-F2018
Head Loss of the Pump in the Fluid Mechanics Laboratory-S2019
Application of Bernoulli’s Principle: Water Shooter Design-Fall208
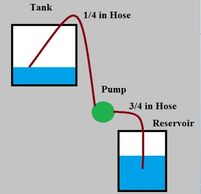
Water needs to get into a house. High rise water towers have the water pumped up into then gravity fed down. Water can be pumped from a well or reservoir below the home and put into a house storage tank for use as needed.
Application of Head Loss in Aluminum Cans-S 2019
Head Loss of the Pump in the Fluid Mechanics Laboratory-S2019
Head Loss of the Pump in the Fluid Mechanics Laboratory-S2019

Various beverage companies have made claims about the openings in their cans and how they improve flow. We know that an increase in the cross-sectional area will allow for more flow, but we wanted to explore how the shape of the opening impacts the flow. To do this, our team created six different shaped openings and measured the flow through that opening on the hydraulic bench. By measuring the difference in height between the centroid of the opening and the level of water in the reservoir, we could determine the efficiency of the shape. Using the collected data, head loss was determined for each shape by the energy equation. Head loss depends on the velocity of the water flowing through the opening, so we needed another parameter. Using the equation for minor head loss, the value for kL was found for each shape. The results showed that a triangular and circular shape had the lowest kL value, and therefore the highest efficiency of flow. The worst result was found to be a rectangular cross-section.
Head Loss of the Pump in the Fluid Mechanics Laboratory-S2019
Head Loss of the Pump in the Fluid Mechanics Laboratory-S2019
Head Loss of the Pump in the Fluid Mechanics Laboratory-S2019

The objectives of the lab were to determine head loss of a pump by using Bernoulli’s equation and to find the horsepower of the pump during the experiment. The procedure included the use of the pump in the open channel system, measuring the lengths of the piping, and counting the number of elbows and valves for total head loss calculations. The head loss of the pump was then calculated using Bernoulli’s Equation, and the horsepower was calculated after that. Schematics for the specific pump used in the experiment were researched online and then compared with the experimental data. When comparing the manufacturer data with the data found during the lab, a relatively large percent error was observed. However, the pump was not run at its ideal efficiency, so some variation in data was expected.
Determine the Head Loss a Piping System-S2019
Effect of Obstructions in a Piping System-S2019
Effect of Obstructions in a Piping System-S2019

The purpose of this lab was to determine the head loss in the piping system that discharges into the open flow channel device in the fluid mechanics' laboratory. Piping systems are implemented across a wide array of industries, including but not limited to wastewater treatment, farm field irrigation, manufacturing, and residential housing. Head loss is a key consideration when designing a piping system because it is a significant contributor to the efficiency of the system. Flow rate and output frequency were measured and recorded. From here the continuity equation, energy equation, and Reynolds number were used to find the pressure at the pump and head loss at the discharge point. The head loss at a pump output of 29 Hz was found to be 2.11 ft. Overall, the experiment showed that the piping system for the open channel flow device is subject to a minimal amount of head loss and the pressure experienced within the system is nearly negligible.
Effect of Obstructions in a Piping System-S2019
Effect of Obstructions in a Piping System-S2019
Effect of Obstructions in a Piping System-S2019

The purpose of this experiment was to determine how obstructions added to a piping system would affect the velocity of a liquid. This was done by screwing screws into a pipe to lower the cross-sectional area of the pipe, causing the velocity to increase. An increased velocity will lead to an increase in major and minor losses. The major losses occurred due to friction within the pipe while minor losses occurred due to contractions in the piping system, a product of the obstructions in the various iterations of the experiment. The friction caused the largest losses in all iterations, while the iteration with the obstruction forming an ‘x’ pattern caused the most minor losses from the increased contraction.
Open Channel Flow Analysis Abstract-S2019
Effect of Obstructions in a Piping System-S2019
Open Channel Flow Analysis Abstract-S2019

Open channel flow is a special type of fluid flow characterized by a flow involving a free surface such as a river, canal, or sewer line. The effects of a sluice gate on the behavior of open channel flow are of interest to engineers. It is desired to determine how the height of a sluice gate affects the velocity, Reynolds number, and head both upstream and downstream of the sluice gate. A variety of sluice gate heights were tested, and the calculations showed that an increase in sluice gate height results in an increase in upstream velocity, Reynolds number, and Froude’s number, a decrease in hydraulic jump, and little impact on downstream velocity and Reynolds number. The results of this experiment allow for a better understanding of the effects of a sluice gate as well as other obstructions within open channel flow.
Site Content
Storm Drainage System-F2019
Comparing Flow Through a Circular and Square Pipe-F2019
Fluid Density and Hydrostatic Force-F2019

A storm inlet is defined as the portion of a storm drainage system that receives runoff and
allows entrance of this runoff to some point where it is then discharged into a channel, body of
water, or piped system. The objective of this lab was to determine the flow and efficiency of
three different designs of storm inlets. The three included circular holes, square holes, and slits.
The lab was constructed by a series of trials that included two sets for each type of storm inlet
design. Each inlet design was experimented and accompanied by obstruction of leaves as well as
unobstructed, to observe the flow and efficiency of each type of storm inlet design. Once these
trials were completed, results were recorded and observed to decide which inlet design would
provide a more efficient and viable option for engineering applications. The results illustrated
that the square holed inlet design would be able to hold up even better than that of the slits.
Fluid Density and Hydrostatic Force-F2019
Comparing Flow Through a Circular and Square Pipe-F2019
Fluid Density and Hydrostatic Force-F2019

Hydrostatic force refers to the resultant force on an object by a fluid and is a function of density and fluid level. The objective of this lab was to determine the different fluid densities of water, 2% milk and vegetable oil, Figure 1, and how each affects the hydrostatic force on a planar and curved surface. The team hypothesized that the fluid with the greater density would yield the greatest hydrostatic force. The experiment was done through a series of 8 trials at 90-degrees and 6 trials at 60-degrees. All results were recorded, compiled, and used to determine the correlation between fluid densities and hydrostatic force. The hydrostatic force apparatus used for the experiment is shown below, Figure 2. The team found that milk had the highest density (1050 kg/m3) followed by water (1000 kg/m3) then oil (900 kg/m3). The hypothesis was found to be true, the hydrostatic force was highest for the milk and lowest for oil, on average, for both the 90 and 60-degree trials.
Comparing Flow Through a Circular and Square Pipe-F2019
Comparing Flow Through a Circular and Square Pipe-F2019

The objective of this lab was to compare multiple aspects of the flow of water through the circular and square tubes using the Reynolds number apparatus in Figure 1 below. The hydrostatic pressure in the holding reservoir was calculated for two different height values and was then used to explore how the height also effects different properties including the pressure in the pipes, the Reynolds number, and the head loss of the system. It was found that the increase in height in the reservoir also increased the pressure, the Reynolds number, and the head loss. This was because the increase in height, increased the velocity and the flow which were both used in calculations that increased the value for each element tested on the apparatus. There was no significant difference between the square and circular pipe’s pressure within the pipes. The Reynold’s number showed the greatest difference between the circular and square pipes. The square pipe yielded consistently higher Reynold’s numbers, and therefore consistently more turbulent flow. All tests yielded results that were congruent with the hypotheses although there were still forms of human and mechanical error in the tests.
Open Channel Flow and Fraction of Mechanical Energy-F2019

The scope of this experiment was to figure out in an open flow channel what would happen if, a gate would impede the fluid inside the channel at various heights. The effects were hypothesized to be that as downstream velocity increases, the discharge coefficient would also increase along with a dissipation of energy as the gate’s height decreased from the bottom of the channel. The experiment consisted of a constant flow through the channel and started off with measurements of the channel such as the height of the water level at various locations along with the base of the channel. The recorded results were used in calculations to determine the fluid mechanic properties such as Specific Energy, Froude’s number, Reynolds number, and hydraulic radius along with others. These calculations proved that as the gate was lowered deeper into the channel, the velocity and coefficient discharge did increase. In addition, the energy of the flow decreases as it had hit the sluice gate.
Coefficient of Drag -F2019
Properties of Fluids that Effect Hydraulics-F2019

The objective of this lab was to calculate the coefficient of drag on a spherical object. In this lab, steel and acrylic beads were used. The beads were dropped into different liquids: water and vegetable oil all at room temperature. Six trials were conducted, three for each liquid using the two different types of beads. The time it took for a bead to fall a certain distance was recorded. The more vicious the liquid was, the higher the coefficient of drag was. The coefficient of drag for the two beads, viscosity and Reynolds numbers of both liquids were calculated. The calculated viscosities were compared to the actual viscosity for water and vegetable oil.
Properties of Fluids that Effect Hydraulics-F2019
Properties of Fluids that Effect Hydraulics-F2019

Understanding the properties of fluids and how they affect the workability of hydraulics, can help determine an optimal hydraulic fluid for use in hydraulic systems. This project’s purpose was to compare properties of fluids and observe the workability of these fluids in a hydraulic crane apparatus. The group built a hydraulic crane apparatus out of cardboard and used syringes connected with plastic tubing to create a hydraulic system. The hydraulic system was then tested with water and oil. Attempts were made to test the system with syrup but were unsuccessful. Based on the observed workability of the hydraulic system with different fluids, it was possible to make conclusions about different fluid properties and their effect on hydraulics. The results showed that the hydraulics were mainly affected by the fluids viscosity and compressibility. Higher viscosities had a lower mechanical efficiency and low viscosities had a higher risk of leakage. Also, high compressibility allowed for higher mechanical efficiency. Overall this project has many real-world applications and was successful in determining properties that effect the mechanical efficiency of hydraulics.
Site Content
Pump Head in a Splash Pad System-F2019
Major and Minor Head Loss in PVC and Copper-F2019
Major and Minor Head Loss in PVC and Copper-F2019

The objective of this lab experiment was to find the pump head and power for a splash pad system using Bernoulli’s equation. ¾’’ PVC pipe was the material used and the system had two elbows, a steel wool filter, and a Y distribution valve. The respective major and minor losses were calculated for the Bernoulli’s equation calculations. Four different flow rates were used to find four pump head values and a graph was generated from the results. This graph was then used to find the appropriately sized pumps to use in future splash pad design systems.
Major and Minor Head Loss in PVC and Copper-F2019
Major and Minor Head Loss in PVC and Copper-F2019
Major and Minor Head Loss in PVC and Copper-F2019

The Purpose of this project was to experiment with the effect of five consecutive 90° bends on a PVC piping system and compare the results to that of the same piping system constructed from copper piping. These two materials were chosen to use for this project due to their frequent use within municipalities, private and commercial, and for their availability along with ease of construction for this arrangement. This project is set up to evaluate the efficiency of the two piping systems in terms of fluid flow along with the cost of materials. The hypothesis in this experiment was that the resulting head loss of PVC pipe would be less than that of copper pipe. The resulting head losses were compiled for PVC pipe with five bends, and these results were compared to the resulting head losses compiled for copper pipe with five bends. The flow was determined and classified for both pipe sections with Reynold’s number and the friction factor for major head loss was obtained from Haaland’s Equation. Figure 1 below shows the piping arrangement used for this project.
Bilge Pump Design-F2019
Major and Minor Head Loss in PVC and Copper-F2019
Straight Drop, Cascading and Vertical Shaft Overflow Spillways-F2019

The team was asked to design a piping system to remove water from the bilge of a boat using a bilge pump. The design team used ¾ inch schedule 40 PVC pipe and 90° PVC elbow for the piping system. The design team found the theoretical headloss from the manufacturers flow rate of the pump and found the headloss to be 4.4 ft. An experiment was conducted to find the actual flow rate of the bilge pump with the piping system and found the actual flow rate to be 523 GPH. The theoretical flow rate of the pump was 750 GPH. From the test results the design team found that the bilge pump was 69.7% efficient. The team was able to recommend this design to be installed on the boat by the client.
Straight Drop, Cascading and Vertical Shaft Overflow Spillways-F2019
Straight Drop, Cascading and Vertical Shaft Overflow Spillways-F2019
Straight Drop, Cascading and Vertical Shaft Overflow Spillways-F2019

Spillways are designed to provide a controlled release of flow and reduce the mechanical energy of water to prevent the damage of a dam. The purpose of this lab was to compare the energy dissipation ratio and coefficient of discharge of a straight drop, cascading, and vertical shaft spillway. This was accomplished by constructing three different spillways to examine the effects in an open channel system. The velocity of the water was recorded on each side of the structure, as well as the height of the water. These values where then used to determine head loss, specific energy, and the coefficient of discharge of the system to compare across the three spillway designs.
Behavior of Water in an Open Channel Over a Bump-F2019
Straight Drop, Cascading and Vertical Shaft Overflow Spillways-F2019
Behavior of Water in an Open Channel Over a Bump-F2019

The behavior of a fluid in an open channel flowing over a bump is something can be characterized using fluid mechanics. Different concepts can be used to determine how high a bump needs to be in order to cause a desired amount of energy loss in a channel. This can be applied in streams and rivers while designing a wing dam to help reduce shore-line erosion by flowing water. Froude’s number describes the character of flow in an open channel and can define flow as being subcritical, critical, or supercritical. The energy dissipation ratio shows how much the obstruction affects the flow in the channel. The objective of this lab was to see how different obstructions in an open channel affect Froude’s number, the energy dissipation ratio, and determine the experimental height of the obstruction in the channel. Three trials were performed for each of the two shapes, a concrete cube and a cylinder, at differing velocities. Velocity data was gathered before and after each concrete shape and water height as well as shape dimensions were recorded. Conclusions from this lab indicate that as the size of the object increases, the energy dissipation ratio increases as well. As the velocity of the water increases, the energy dissipation ratio decreases. The Froude’s Number should that the flow in the channel was subcritical, and the Froude’s Number over the bump was very close to 1 and critical. The experimental values for the height of the bump in the channel were found and had a percent error of 81%-128%. This is most likely due to inaccurate equipment and readings during the lab.
Variation of Pressure and Flow in Sprinkler Piping-F2019
Straight Drop, Cascading and Vertical Shaft Overflow Spillways-F2019
Behavior of Water in an Open Channel Over a Bump-F2019

The objective of this experiment is to evaluate and design a water delivery system for a fire suppression or yard sprinkler. Bernoulli’s equation would be used to calculate the expected overall changes in energy and compare them to changes measured in the experiment. The process included the use of a single PVC pipe with several holes drilled into its side (seen in Figure 1 below), which water would sequentially flow out of. The heights, dimensions, positions, outflow velocities, and pressures recorded at each of these locations were then used to determine the differences in resulting head at the end of the system. These losses were then compared to expected changes in pressure and velocity heads using Bernoulli’s equation. Changes in pressure occurred similarly to predicted trends with variations only occurring due to other losses throughout the system. Velocity head gradually increased over the length of the piping, due to errors in the design of the pipe, but changes in flow rates as holes were blocked provided data agreed with theoretical values. Overall the pipe would need to be heavily modified for use in an actual fire safety system.
Project Video Ram Pump
Ram Pump video (mp4)
DownloadVideo
PROJECT VIDEO- MAJOR AND MINOR HEAD LOSS -Fall 2019